锥齿轮节锥距的模拟检测及其变差分析

　　关键词：锥齿轮 节锥距 模拟法 测量 变差分析

　　【 摘要：本文根据锥齿轮齿形特点，运用模拟法的原理，抽象出直齿锥齿轮的节锥，同时根据生产实际，通过基准转换间接地测量出锥齿轮的节锥距，并运用微分的原理对该种间接测量进行了精度分析，给出了变差范围，较好地解决了节锥距这一理论尺寸不便于检测的难题。】

　　Abstract: According to the bevel gear tooth shape characteristic and the principle of using the simulation method, This paper abstracts the quarter spur bevel gear cone, whilst based on the production practice, through the datum transformation indirectly measured out the quarter from bevel gear cone, and using the principle of differential for this indirect measurement of the precision analysis, give the worse range, better solve the quarter difficult problems that failed to test with this theory.

　　Key Words: bevel gear quarter from the simulation method become poor cone measurement analysis

　　一、锥齿轮关键尺寸的重要性

　　我公司为汽车前后桥专业化生产企业，车桥减速器总成中有一套差速器装置，其中就有一对半轴齿轮，属直齿锥齿轮，齿形为渐开线，如图一。在差速器总成的实际装配过程中，常常因为节锥距(图中35.5的尺寸)超差，引起装配不合格。如尺寸偏小，则差速器齿侧间隙加大，造成汽车转向时噪音加大，严重时出现齿面磨损加剧，轮齿折断，引起主减总成全部报废。如尺寸偏大，则造成装配过紧，无齿侧间隙，差速器不工作，严重时引起各零件温度升高，配合部位磨损异常，同样影响差速器总成的正常寿命。

　　二、对锥齿轮的检测

　　由于节锥距是齿轮节锥顶点到齿背大平面之间的距离，节锥顶点为一虚点，无法直接测量。为解决上述问题，在没有齿形参数

　　专用检具的前提下，设计了一套该尺寸的模拟测量用检具。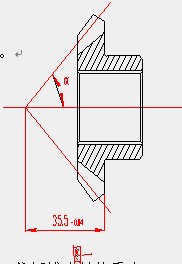

　　如图二，图中1 检验托盘，2 定位钢球，数量3件。

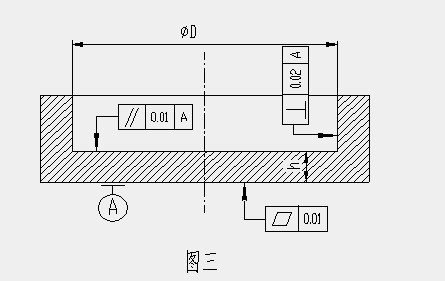
　　零件示意图如图三

　　检测时，先将检验托盘置于检验用平台

　　上，根据半轴齿轮的特点将3件钢球呈等边三

　　角形或等腰三角形或大致等腰三角形均匀放置，

　　再将半轴齿轮齿形面放置于上述3件钢球上，

　　调整半轴齿轮以使3件钢球均匀落入锥齿轮的齿廓凹槽内，依托锥齿轮的重力

　　作用，使钢球与托盘φD内孔壁接触。然后用杠杆百分表将A面校平，并测出

　　A面至平台的高度K值。

　　现在根据检测结果，核算图一中35.5尺寸，原理及计算结果如下：

　　先假定图中钢球已模拟出锥齿轮的节锥，且节锥角α按图一所示不变。

　　如图四，根据图中的几何关系，

　　AB=d/2×Cosα

　　BD= d/2×Sinα

　　CA=D/2-AB-d/2= D/2-d/2×Cosα-d/2

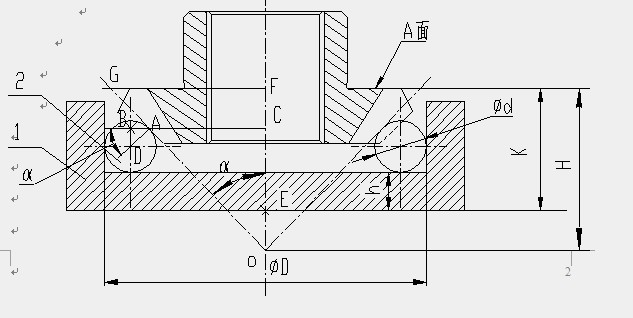
　　OC=CA/tanα

　　CE=h+d/2+BD

　　OE=OC-CE

　　=(D/2- d/2×Cosα-d/2)/tanα- (h+d/2+d/2×Sinα) …………(1)

　　则：H =OE+ K…………………………………………………………………(2)

　　上述(1)式中，由于OE通过托盘直径D、底座厚度h、钢球直径d，及齿轮节锥角计算得出，K值可直接测量，则节锥距H便相应计算得出。

　　值得注意的是，上式中计算出的H 值,并不是图一中真正的35.5尺寸。因为上式是假定钢球已模拟接触到了锥齿轮节锥。而实际情况是很难准确地模拟到的。但是根据锥齿轮的齿形及钢球的特点，此处可以模拟到一类似的“节锥”，此节锥的节锥距即为上式计算所得的H值。

　　将上述检测出K值的锥齿轮应用到实际装配过程中，如装配合格，则此K值可作为检验用的模拟标准值，该齿轮为检验用的标准齿轮。其它齿轮是否合格以其K值与该标准齿轮K值相比较，从而作出合格性判定。

　　三、标准齿轮K 值的变差分析

　　在现代批量生产和加工过程式中，锥齿轮K值不可能完全一致。根据锥齿轮的加工特点，从经济性出发，K值总是存在于一合适的范围之中。为不产生误判，就必须弄清K值合理的变差范围。下面根据齿轮节锥距的设计公差导出模拟标准K值的变差。

　　参见图二，假定H尺寸变差为ΔT，根据几何关系，则：

　　FG/OF= tanα 有：

　　ΔFG/ΔT=tanα………………………………………………………(3)

　　ΔFG：尺寸FG的变差。

　　根据相似三角形的关系：FG/CA=OF/OC

　　因OF和OC的名义尺寸已经测出或导出，这里假定其比值为n，则有：

　　ΔCA/ΔT= tanα/n 令ΔCA为ΔX 有

　　ΔX/ΔT= tanα/n

　　再根据图二中的几何关系：

　　由于CA= D/2-d/2×Cosα-d/2

　　运用微分原理，ΔX与钢球直径d的增量Δd的关系为：

　　ΔX/Δd=-1/2×(1+Cosα)…………………………………………(4)

　　即：Δd/ΔX=-2/(1+Cosα)………………………………………(5)

　　再根据上式中K = H-OE，即

　　K= H-(D/2- d/2×Cosα-d/2)/tanα +(h+d/2+d/2×Sinα)

　　则：

　　ΔK/Δd= 1/2[(Cosα+1)/tanα+1+Sinα]…………………………(6)

　　根据上式(3)、(5)、(6)即得：

　　ΔK/ΔT =ΔK/Δd×Δd/ΔX×ΔX/ΔT

　　运用上式，再根据锥齿轮T值的变差ΔT便可计算出ΔK值，即模拟标准K值的变差范围。

　　四、实例计算

　　如某半轴齿轮齿数Z=20，端面模数m=4.973，最大外径为φ101，节锥角α=63.43°，理论节锥距T为35.5，上偏差为0，下偏差为-0.04，

　　故根据此锥齿轮外圆及端面的基节大小，选定托盘内径D为φ110，钢球直径d为1/2″，底面高h=10，则：

　　在上述条件下，测出的K=34.0

　　(1)节锥距的计算：

　　AB=d/2×Cosα=2.84

　　BD= d/2×Sinα= 5.68

　　CA=D/2-AB-d/2= D/2-d/2×Cosα-d/2=45.97

　　OC=CA/tanα=23

　　CE=h+d/2+BD=22.03

　　OE=OC-CE=0.97

　　H =OE+ K =34.97

　　即：检测的节锥距为34.97，该值与理论尺寸存在差异的原因是模拟的节锥并不是理论节锥。

　　(2)K值变差分析：

　　n= OF/OC=34.97/23=1.52

　　ΔX/ΔT= tanα/n=1.316

　　Δd/ΔX=-2/(1+Cosα)=-1.38

　　ΔK/Δd= 1/2[(Cosα+1)/tanα+1+Sinα]=1.31

　　ΔK/ΔT=1.316×-1.38×1.31=-2.38

　　ΔK=-2.38×0.04=-0.10(变差ΔT即是T 值公差，负值表示公差为反方向)

　　此ΔK值即为模拟标准齿轮的K值变差范围。

　　(3)K值的合格范围

　　通过计算：

　　K值在34.0 -34.10范围内均是合格品。

　　五、使用效果与结论

　　随着我公司前后桥总成的不断开发，各种型号的半轴齿轮越来越多，为了杜绝主减异响、齿轮早期磨损及主减不差速等质量问题，该尺寸的有效检测显得尤为重要。对于各种型号的半轴齿轮都可以应用以上模拟检测方法，并根据设计要求计算各型号齿轮K值的变差范围。该检测方法的引入，能正确有效地对产品的进行合格性判定，使得产品质量得以很好的控制。

　　主要参考文献：

　　《机械设计手册》 徐灏等主编，机械工业出版社。

　　《齿轮手册》上册 叶克明等主编，机械工业出版社。