运用GPS测定地面点高程方法的研究

　　摘要：用GPS可以精确地测定三维坐标X，Y，Z和大地高差H,利用GPS测得的大地高结合现有的水准资料可求出具有正常高h的GPS点的高程异常，再用数字拟合法，可计算出其它GPS点的高程异常和正常高。本文结合具体实例，介绍和分析利用GPS测定地面点高程的方法和达到的精度。

　　关键词：GPS大地高，高程异常，高程拟合，数学模型

　　Abstract: using GPS can measure exactly 3 d coordinate X, Y, Z and the earth difference H, using GPS measurement of the earth with high level of existing data for a normal high H GPS point of abnormal height, garnish with digital intends to legal, may be calculated other GPS point of abnormal height and normal high. This paper based on some examples, introduction and analysis to determine the ground using GPS point of methods and achieve elevation accuracy.

　　Keywords: GPS the earth is high, the abnormal height, elevation fitting, the mathematical model

　　中图分类号：P228.4 文献标识码：A 文章编号：

　　0 引言

　　由GPS相对定位得到的三维基线向量,通过GPS网平差,可以得到高精度的大地高差。如果网中一点或多点具有精确的WGS-84大地坐标的大地高程,则在GPS网平差后,可求得GPS点的WGS-84大地高程。实际应用中,地面点的高程采用正常高系统,正常高Hr是地面点延铅垂线至似大地水准面的距离。是通过水准测量的方法来确定的,这就需要确定大地高与正常高的关系。似大地水准面与参考椭球面间的高差即高程异常,有Hr=H84-ζ,其中Hr为正高。高程拟合方法的基本思路是:在GPS网中联测一些水准点(要求这些点分布均匀、密度充分),再利用这些点上的正常高和大地拟合高求出它们的高程异常值,再据这些点上的高程异常值与坐标的关系,用最小二乘方法拟合测区的似大地水准面,利用拟合的似大地水准面内插入其它GPS点的高程异常,从而求出各个未知点的正常高

　　1 GPS测定地面点高程的原理和拟合法数学模型

　　我国高程系统采用的是正常高系统，在工程建设中我们常常用到的地面点高程是地面点到大地水准面的距离，即正常高h，而GPS测定的是地球地心直角坐标系中的基线向量三维坐标差。经过GPS网三维平差后，可获得GPS点的大地高H,因此地面两点的正常高之差Δh与大地高之差ΔH的关系为：

　　Δh=ΔH-Δζ Δζ为似大地水准面高之差，即两点高程异之差。

　　上式中的ΔH可由GPS相位测量精确测定，若要获得地面两点正常高之差Δh，首先要求解出Δζ，因此求解高程异常ζ是GPS测定高程的主要问题。

　　由上式可知，GPS网三维最小约束平差后可得到各点大地高Hi，如果我们在GPS网中进行一些水准测量或联测部分水准高程点，那么就可得到该点的正常高hi,求改点的高程异常ζi 有公式：ζi=Hi-hi

　　若把GPS和水准测量共测点所得到的ζi为已知，再用数学模型拟合其它点高程异常，从而可求得其它点的正常高。

　　1.1曲线拟合

　　当GPS点按线状布设时,我们可以根据水准重合点的平面坐标和高程异常,拟合出线方向上的似大地水准面曲线,解求插值点的高程异常。若将坐标系转换成x与测线方向重合,y与测线方向垂直,则设ζ和x间存在下述函数关系:ζm(x0)0=a0+a1 x i+a2 x i2+…am xim;在已知点处的高差Ri=ζm(xi)-ζi;在∑Ri2=min条件下解各ai,继而求出各点的Hr。当测线长、已知点多、ζ变化大时,按∑Ri2=min解求的ai误差会增大,故通常总采取分段计算。这样使曲线在分段点下连续,也影响拟合精度,故采用三次样条法来拟合。

　　1.2曲面拟合

　　当GPS点布成一定区域面时,可采用数学曲面拟合求待定点的正常高。即根据测区中已知点的平面坐标x,y(或大地坐标B,L)和ζ值,用数值拟合法,拟合出测区似大地水准面再内插出待求点的ζ,从而求出待求点的正常高。设测站点的高程异常ζ与坐标x,y间存在以下函数关系:ζi=f(x i,yi)+εi式中:f(xi,yi)为ζ的趋势值;εi为误差。选用空间曲面函数:f(xi,yi)=a0+a1xi+a2 yi+a3xi2+a4xiyi+a5yi2+a6xi3+a7xi2yi+a8xiyi2+a9yi3进行拟合,ai为待定参数。于是,有:ζi=a0+a1 xi+a2 yi+a3 xi2+a4 x i yi+a5 yi2 a6 xi3+a7 xi2+a8 x i yi2+a9 yi3+εi (I=1,2,……,m)式中:m是重合点数。当m大于或等于待定参数ai时,可在[ε2]=min的条件下,求出参数ai,进而求出测区内任意插值点的高程异常值。

　　2 测区GPS网高程拟合方法和精度

　　2.1本溪县测区GPS网

　　本溪县城区 GPS网主要是为大比例尺测图解决平面基础控制。网中由35个点组成，控制面积约25平方公里，我们观测的同时，又在15个GPS点上施测四等水准，这些点在GPS控制网中基本分布均匀。

　　GPS外业观测结束后，对观测数据预处理并组成GPS基线向量。用GPS后处理软件对GPS网进行三维最小约束平差。以获得个点的大地高Hi，在由15个水准点的高程值hi，可得到这些点的高程异常ζi。

　　表1

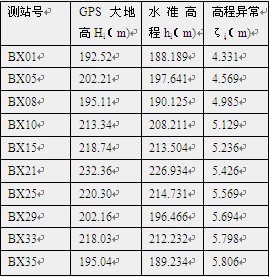
　　由表中可以看出，本测区的内似大地水准面差距ζi由东向西逐渐变大，变化幅度大约为每公里增大5cm，南北变化不是很明显，并且在测区内没有发现高程异常大的变动，表明测区内似大地水准面曲线变化比较平缓，但考虑控制面积较大，所以在GPS网周围和中部选择了8个水准高程点用作高程控制，进行二次曲面拟合和GPS高程网平差。平差后GPS点高程中误差最大为±2.1cm,与测区内其它一些四等水准高程比较见表2

　　表2

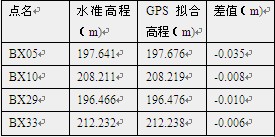
　　3 GPS网高程平差中对水准控制点 的选择和平差方法

　　运用一次或二次多项式数学模型进行测区大地水准面差距拟合，其可靠性也选择的高程控制点在网中的分布有较大关系，因此GPS网中选择合适的高程控制起算点很重要，若不适当，用同级相同个数的高程拟合平差，其结果差别明显。如在本溪县城GPS网中，若选择08,11,16,20四个测站点的水准高程来进行平面拟合(这四个点分布在网的东南部，不覆盖全网)，平差后高程就增加到±0.028cm。

　　在表1列出的高程异常值中我们还发现，GPS网中点的分布在南北走向上一致，即点的横坐标值接近时，这些点的高程异常值相差非常小，在相距5公里以内的地面两点四似大地水准面高之差Δζ小于±3cm，由公式Δh=ΔH-Δζ可得，Δh=ΔH±0.03。因此，在地势起伏不大的测区，南北一致的GPS点(东西摆动不超过2公里)，直接用GPS测定的高差代替水准高差来推算高程值，精度可达到±3cm。当然，想达到此精度的前提是推算高差的GPS基线向量的质量要可靠，仪器或接收机天线量高要准确。

　　另外，我们施测GPS控制网，一般都是解决平面精度为主，往往要联测测区外高等级控制点，这样就会造成GPS网控制面积增大，在GPS高程网平差时最好将那些在测区外的一些点撇开，这样使高程控制点在小范围内模拟大地水准面会更可靠，大网也可以使用分区平差的方法。

　　4 结束语

　　上述GPS网高程转换的精度表明，在地形比较平坦的地区，GPS高程转换采用曲面拟合法，高程精度可达到±8cm以内，若是局部小范围的GPS控制网，采用平面或曲面拟合，GPS高程可代替四等水准测量。

　　总之，GPS测量能以很高的精度同时获取测站点的三维坐标，如果我们只是利用其中的平面位置信息，这无疑是种浪费。通过实例说明，只要采取一定的方法和手段，利用GPS测量中的高程信息解决地面点高程，可获得较好的效益，可大大减少常规测量的费用和劳动量。

　　参考文献：

　　[1] 孔祥元，郭际明，刘宗泉编著，大地测量学基础，武汉大学出版社，2001.

　　[2]徐绍铨，等.GPS测量原理与应用，武汉测绘科技大学出版社，2000

　　[3]徐绍铨.GPS高程拟合系统研究。武汉测绘科技大学学报，1999,12